私が小学五年生の時（三角形の面積を学習した時）に考え付いた簡単な公式を、一つ紹介しようと思う。次の図を、見て頂きたい。８個並んでいる図を、左上から右下にかけて図１、図２…図８とする。

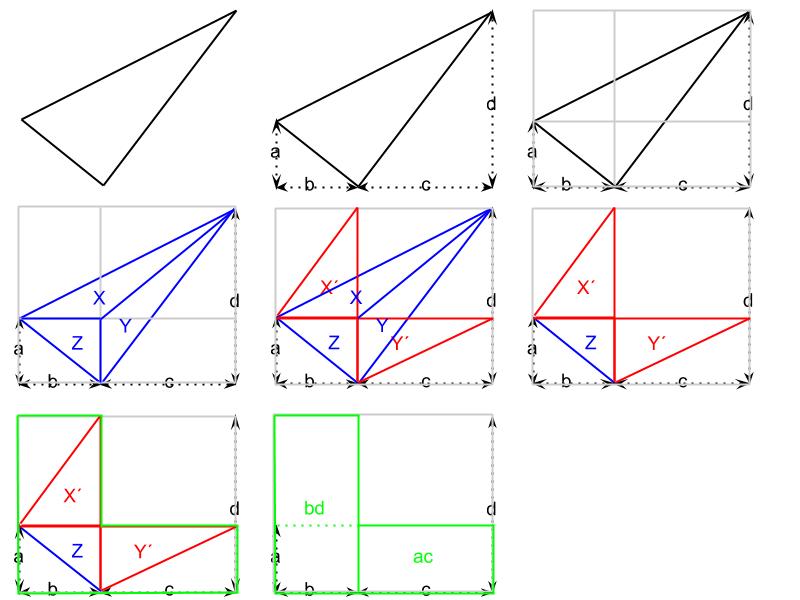
　図１の三角形に対し、a~dと長さを定める（図２）。すると、三角形の面積Sは、

で求める事が出来る。以下、その理由を説明する。
　まず、図３の様に、三角形に外接する長方形と、その長方形の各辺に直交する二つの頂点を通る直線を引く（灰色の線）。また、この三角形は、図４の様に三つの三角形X,Y,Xに分ける事が出来る。図５で、XとX’、YとY’は底辺と高さが同じ三角形だから、面積は等しくなる。また、この事より、”(X+Y+Z)=(X’+Y’+Z)”が言えるから、元の三角形の面積は、図６に示された図形の面積と等しくなる。図６の三つの三角形は、図７で示した黄緑色のＬ字型の部分の面積の半分になる。また、図８から分かる通り、黄緑色のＬ字型の部分の面積は、”ac+bd”で求める事が出来る。以上の事より、求める三角形の面積は、黄緑色のＬ字型の部分の面積”ac+bd”の半分であるから、上記の公式が成り立つ。

　ちなみに、ａとｄを底辺（上底・下底）とした台形から、三角形２つ― ａとｂ、ｃとｄを底辺・高さとする直角三角形 ―分の面積を引いた方が、証明としては簡潔である。しかしながら、この公式を考え付いた当時は、まだ台形の求積式を知らなかった。よって、この様な煩雑な証明となってしまった次第である。